As promised, here's the solution to the ladder puzzle I posted recently.
Ten people sent in correct solutions (congratulations!); some were different
from mine, but still based on the same basic ideas, although some used
trigonometry. One person even reported being able to solve it mentally, which,
as promised, impressed me. I still haven't seen a solution without calculus,
but I believe it's possible.
Anyhow, since I'm too lazy to try to get mathematics look good in HTML, here's
a PNG from LaTeX:

Inspired by a comment from a co-worker, I pondered the following puzzle --
I'm quite sure it's well-known already, but I don't know its name, and it
was fun anyway. (It's solvable with only high school maths, but I cheated and
used Maple, since my algebra manipulation skills have dwindled to near-nothing.
You'd want pen and paper, though -- if you're able to do it mentally I'm
impressed.)
Assume you have a ladder (or, a line segment if you will), conveniently of
length 1, put up against a vertical wall. Depending on the angle, you could
have several different curves, some of which have been overlaid below:
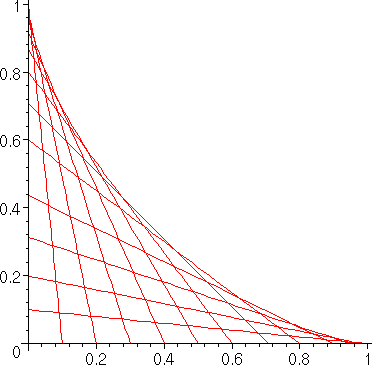
As you can see, the exterior of this figure follows a nice, smooth slope.
Now, the question is: What is the formula for this exterior curve?
Solutions accepted by e-mail, Planet Debian or IRC. No prizes, only fame :-)
Update: I forgot to say, I'll post the solution in a few days.
Update 2: Five people have sent in solutions so far, of which only one was
right. The other four have suggested it's a quarter-circle; it's not, as you
can see from this picture.
You can stop sending in that as an attempted solution :-)

