Inspired by a comment from a co-worker, I pondered the following puzzle -- I'm quite sure it's well-known already, but I don't know its name, and it was fun anyway. (It's solvable with only high school maths, but I cheated and used Maple, since my algebra manipulation skills have dwindled to near-nothing. You'd want pen and paper, though -- if you're able to do it mentally I'm impressed.)
Assume you have a ladder (or, a line segment if you will), conveniently of length 1, put up against a vertical wall. Depending on the angle, you could have several different curves, some of which have been overlaid below:
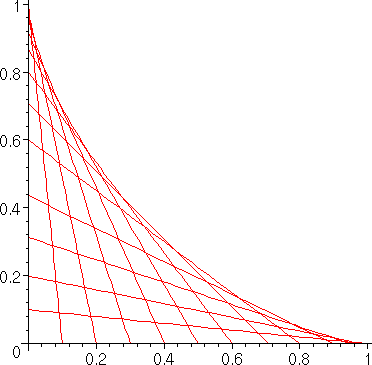
As you can see, the exterior of this figure follows a nice, smooth slope. Now, the question is: What is the formula for this exterior curve?
Solutions accepted by e-mail, Planet Debian or IRC. No prizes, only fame :-)
Update: I forgot to say, I'll post the solution in a few days.
Update 2: Five people have sent in solutions so far, of which only one was right. The other four have suggested it's a quarter-circle; it's not, as you can see from this picture. You can stop sending in that as an attempted solution :-)