We recently renumbered (for the first, and I hope the last time), and in the
process, the question of IPv6 adressing came up; how do you assign static
IPv6 addresses within a given /64?
I won't be going into the full discussion of the various different
strategies, but I'll say that one element of the solution chosen was that
if you had an IPv4 address ending in .123, you'd also get an IPv6 address
ending in ::123. (IPv6-only hostnames would be handled differently.)
But then, how do you make sure the reverses are in sync? For some reason,
BIND doesn't have a good way of synthesizing a PTR name from an IPv6 address,
so you're stuck with typing 3.2.1.0.0.0.0.0.0.etcetcetc and hope you got
everything right. It's a pain.
So instead, behold:
$ORIGIN 0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.4.f.9.2.c.7.6.0.1.0.0.2.ip6.arpa.
$GENERATE 1-9 $.0.0 CNAME $.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.1.0 CNAME 1$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.2.0 CNAME 2$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.3.0 CNAME 3$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.4.0 CNAME 4$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.5.0 CNAME 5$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.6.0 CNAME 6$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.7.0 CNAME 7$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.8.0 CNAME 8$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.9.0 CNAME 9$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.0.1 CNAME 10$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.1.1 CNAME 11$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.2.1 CNAME 12$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.3.1 CNAME 13$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.4.1 CNAME 14$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.5.1 CNAME 15$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.6.1 CNAME 16$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.7.1 CNAME 17$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.8.1 CNAME 18$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.9.1 CNAME 19$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.0.2 CNAME 20$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.1.2 CNAME 21$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.2.2 CNAME 22$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.3.2 CNAME 23$.52.35.193.in-addr.arpa.
$GENERATE 0-9 $.4.2 CNAME 24$.52.35.193.in-addr.arpa.
$GENERATE 0-4 $.5.2 CNAME 25$.52.35.193.in-addr.arpa.
and voila:
pannekake:~> host 2001:67c:29f4::50
0.5.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.4.f.9.2.c.7.6.0.1.0.0.2.ip6.arpa is an alias for 50.52.35.193.in-addr.arpa.
50.52.35.193.in-addr.arpa domain name pointer pannekake.samfundet.no.
Instant IPv4/IPv6 sync.
One of the topics that has come up a few times during the development
of Movit (my high-performance, high-quality video filter library)
is the one of color and color spaces. There's a lot of information out there,
but it took me quite a while to put everything together in my own head.
Thus, allow me to share a distilled version; I'll try to skip all the detail
and the boring parts. Color is an extremely complex topic, though; the more
I understand, the more confusing it becomes. Thus, it will probably become
quite long.
What is color?
Color is, ultimately, the way our vision reacts to the fact that light
comes in many different frequencies. (In a sense, the field of color is
actually more a subfield of biology than of physics.) In its most exact form,
you can describe this with a frequency spectrum. For instance, here is
(from Wikipedia) a typical spectrum of the sky on a clear summer day:

However, human eyes are not spectrometers; there are many colors with
different frequency spectra that we perceive as the same. Thus, it's useful
to invent some sort of representation that more closely corresponds to
how we see color.
Now, almost everybody knows that we represent colors on computers with
various amounts of red, green and blue. This is correct, but how do we
go from those spectra to RGB values?
XYZ
The first piece of the puzzle comes in the form of the CIE 1931 XYZ color
space. It defines three colors, X, Y and Z, that look like this
(again Wikipedia; all the images in this post are):

Don't be confused that they are drawn in red, green and blue, because they
don't correspond to RGB. (They also don't correspond to the different cones
in the eye.)
In any case, almost all modern color theory starts off by saying that
describing frequency spectra by various mixtures of X, Y and Z is a good
enough starting point. (In particular, this means we discard infrared
and ultraviolet.) As a handy bonus, Y corresponds very closely to our
perception of overall brightness, so if you set X=Z=0, you can describe
a black-and-white picture with only Y. (This is the same Y as you might
have seen in YUV or YCbCr. Let me ignore the distinction between Y and Y'
for now.)
Actually we tend to go one step further when discussing color, since we
don't care about the brightness; we normalize the XYZ coordinates so that
x+y+z=1, after which a color is uniquely defined with only its x and y
(note that we now write lowercase!) values. (If we also include the
original Y value, we have the full description of the same color again,
so the xyY color space is equivalent to the XYZ one.)
RGB and spectral colors
So, now we have a way to describe colors in an absolute sense with
only three numbers. Now, we already said earlier, usually we do this
by using RGB. However, this begs the question: When I say “red”,
which color do I mean exactly? What would be its xy coordinates?
The natural answer would probably be some sort of spectral color.
We all know the spectral colors from the rainbow; they are the ones
that contain a single wavelength of light. (Then we start saying
stupid things like “white is not a color” since it is a mixture of
many wavelengths, conveniently ignoring that e.g. brown is also
a mixture and thus not in the rainbow. I've never heard anyone
saying brown is not a color.) If you take all the spectral values,
convert them to xy coordinates and draw them in a diagram, you get
something like this:

(To be clear, what I'm talking about is the big curve, with markings
from 380 nm to 700 nm.)
So now, we can define “red” to be e.g. light at 660 nm, and similar
for green and blue. This gives rise to a gamut, the range of colors
we can represent by mixing R, G and B in various amounts. For instance,
here's the Rec. 2020 (Rec. = Recommendation) color space, used in
the upcoming UHDTV standard:

You can see that we've limited ourselves a bit here; some colors
(like spectral light at 500 nm) fall outside our gamut and cannot
be represented except as some sort of approximation. Still, it's pretty good.
For a full description, we also need a white point that says where we
end up when we set R=G=B, but let me skip over the discussion of
“what is white” right now. (Hint: Usually it's not “equal amount
of all wavelengths”.) There's also usually all sorts of descriptions
about ambient lighting and flare in your monitor and whatnot—again, let
me skip over them. You can see the white point marked off as “D65” in
the diagram above.
A better compromise
You might have guessed by now that we rarely actually use spectral
primaries today, and you're right. This has a few very important reasons:
First, it makes for a color space that is very hard to realize in practice.
How many things to do you know that can make exactly single-frequency
light? Probably only one: Lasers. I'm sure that having a TV built
with a ton of lasers would be cool (*pew pew*!), but right now,
we're stuck with LCD and LED and such. (You may have noticed that
outside a certain point, all the colors in the diagram look the
same. Your monitor simply can't show the difference anymore.)
You could, of course, argue that we should let it be the monitor's
problem to figure out what do to with the colors it can't represent,
but proper gamut mapping is very hard, and the subject of much research.
Second, the fact that the primaries are far from each other means that
we need many bits to describe transitions between them smoothly.
The typical 8 bits of today are not really enough; UHDTV will be done
with 10- or 12-bit precision. (Processing should probably have even more;
Movit uses full floating-point.)
Third, pure colors are actually quite dim (they contain little energy).
When producing a TV, color reproduction is not all you care about; you also
care about light level for e.g. white. If we reduce the saturation of our
primaries a bit (moving them towards the white point), we make it easier
to get a nice and bright output image.
So, here are the primaries of the sRGB color space, which is pretty
much universally used on PCs today (and the same primaries as Rec. 709, used for
today's HDTV broadcasts):
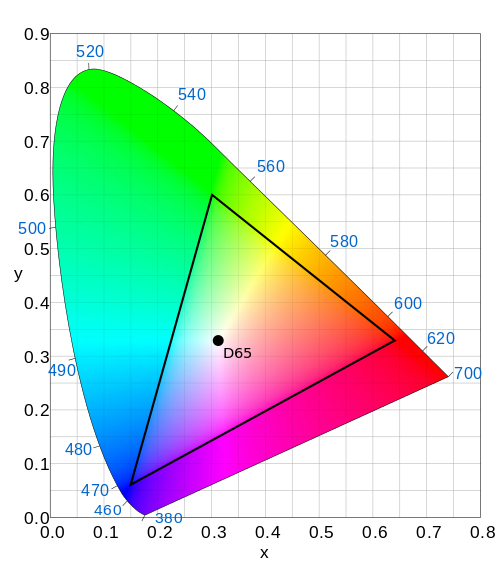
Quite a bit narrower; in particular, we've lost a lot in the
greens. This is why some photographers prefer to work in a wider color
space like e.g. Adobe RGB; no need to let your monitor's limitations come between what your
camera and printer can do. (Printer gamuts are a whole new story, and they
don't really work the same way monitor gamuts do.)
Color spaces and Movit
So, this is why Movit, and really anything processing color data,
has to care: To do accurate color processing, you must know what
color space you are working in. If you take in RGB pixels from
an sRGB device, and then take those exact values and show on an
SDTV (which uses a subtly different color space, Rec. 601),
your colors will be slightly off. Remember, red is not red.
sRGB and SDTV are not so different, but what about sRGB and Rec. 2020?
If you take your sRGB data and try to send it on the air for UHDTV,
it will look strangely oversaturated.
You could argue that almost everything is sRGB right now anyway,
and that the difference between sRGB and Rec. 601 is so small
that you can ignore it. Maybe; I prefer not to give people too many
reasons to hate my software in the future. :-)
So Movit solves this by moving everything into the same colorspace
on input, and processes everything as sRGB internally. (Basically what
you do is you convert the color from whatever colorspace to XYZ,
and then from XYZ to sRGB. On output, you go the other way.)
Lightroom does something similar, only with a huge-gamut colorspace
(so big it includes “imaginary colors”, colors that can't actually be represented
as spectra) called Pro Photo RGB; I might go that way in the future, but currently,
sRGB will do.




